Sönümlü Serbest Titreşim
Aşağıda sönümlü serbest titreşim ile ilgili genel bilgiler paylaşılmıştır.
Bu konu ile ilgili çözümlü bir örneğe buradan ulaşabilirsiniz.
Şimdi sisteme kütlenin hızıyla orantılı olarak kuvvet üreten viskoz bir sönümleyici ekliyoruz.Sönümleme viskoz olarak adlandırılmaktadır çünkü bir akışkanın içindeki bir objeyi modellemektedir. Orantı sabiti “c” sönüm katsayısı olarak adlandırılır ve kuvvet/hız birimindedir(lbf s/ in veya N s/m).
Kütle üzerindeki kuvvetleri toplayarak aşağıdaki adi diferansiyel denklemi elde ederiz:
Bu denklemin çözümü sönümün miktarına bağlıdır. Eğer sönüm yeterince küçükse sistem titreşecek fakat zaman geçtikçe titremesi sona erecektir. Bu durumda sistem az sönümlü olarak ifade edilir—titreşim analizinin en çok ilgi çeken kısmıdır. Eğer sönümü sistemin artık salınmadığı noktaya kadar arttırırsak kritik sönüme ulaşmış oluruz(eğer sönümü kritik sönümün üzerine de çıkarırsak sistem aşırı sönümlü sistem olarak adlandırılır). Kütle yay sönüm modelinde kritik sönüm için sönüm katsayısının ulaşması gereken değer şudur:
Sistemdeki sönümü tanımlamak için sönüm oranı(sönüm faktörü ve % kritik sönüm de denir) denen bir oran kullanılır. Bu oran sistemdeki gerçek sönümün, kritik sönüme ulaşması için gereken sönüme oranıdır. Kütle yay sönüm modeli için sönüm oranı (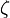
) formülü ise şöyledir:
Örneğin; metal yapılar(uçak gövdeleri, motor krank milleri gibi) 0.05 den daha küçük sönümleme faktörlerine sahipken, otomotiv süspansiyonları 0.2-0.3 aralığındadır.
Az sönümlü kütle yay sönüm sistemi için çözüm aşağıdaki gibidir:
Başlangıç genliği “X” ve faz farkı 
yayın ne kadar sıkıştırıldığına göre değişir. Bu değerlerin formülleri referanslarda bulunabilir.
Bu çözümde fark edilmesi gereken önemli nokta eksponansiyel terim ve kosinüs fonksiyonudur. Eksponansiyel terim sis temin ne kadar hızlı sönümleceğini belirleyen terimdir-sönüm oranı büyüdükçe sistem daha hızlı sönümlenir. Koisinüs fonksiyonu ise çözümün salınım yapan kısmıdır ve salınımın frekansı sönümsüz durumdan farklıdır.
Bu durumdaki frekansa sönümlü doğal frekans, 
, denir ve aşağıdaki formüle göre sönümsüz doğal frekansla ilişkilidir:
Sönümlü doğal frekans sönümsüz doğal frekanstan daha düşüktür, fakat birçok pratik durumda sönüm oranı göreceli olarak küçüktür ve bu yüzden aradaki fark göz ardı edilebilir. Bu yüzden sönümlü ve sönümsüz tanımlamalar, doğal frekanstan bahsedildiğinde, büyütülmüş olur. (Örneğin: 0.1 lik sönüm oranında; sönümlü doğal frekans sönümsüz doğal frekanstan %1 küçüktür.)
Yandaki çizimler 0.1 ve 0.3 lük sönüm oranlarının zaman geçtikçe sistemin sönümlenmesini nasıl etkilediğini gösterir. Pratikte sıklıkla yapılan ise bir darbeden sonra (örneğin; bir çekiçle vurduktan sonra) deneysel olarak serbest titreşimi ölçmektir ve bundan sonra salınım oranını ölçerek sistemin doğal frekansı hesaplanır ve düşüş oranı ölçülerek sönüm oranı bulunur. Doğal frekans ve sönüm oranı sadece serbest titreşimde önemli değildir. Aynı zamanda sistemin zorlama altındaki titreşiminde nasıl davranacağını da belirlerler.
